Ramdon

伪随机数

在大部分的程序语言中，随机数的生成都是伪随机的。什么是伪随机呢？伪随机性（Pseudorandomness）是指一个过程看起来是随机的，但实际上不是。它通常是使用一个确定性的算法计算出来的似乎是随机的数字，我们只要确定算法计算过程中的初始值，那么计算得到的随机数将会是固定的。

如果要获得真正的随机数，那么仅仅依靠软件去生成随机数是不够的，还需要一些随机的事件得到对应的参数指标，例如在 Linux 中获取随机数的方式就是依靠 intel CPU 电路中的热噪声信号产生的随机数，或者是用户的键盘输入的位置速度，大气中的噪声等方式获取真正的随机数，但都是依赖于专业的设备硬件。

伪随机算法

• 线性同余方法（Linear Congruential Generator）LCG
• 梅森旋转算法（Mersenne twister） MT
• M-sequence（Maximum length sequence） MLS
  
  

LCG

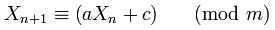
随机数的生成采用了递归公式，这里的 $ X_n $ 表示第 n 个数，$ X_n+1 $ 表示由上一个随机数得到的当前数值，变量 a, c, m 都是常数，LCG 的周期最大为 m，但大部分情况下都会小于 m，要令 LCG 达到最大周期，需要满足以下条件：

1. c，m 互为质数
2. m 的所有质因数都能被整除 a - 1
3. 如果 m 是4的倍数，那么 a - 1 也是
4. a, c, n都比 m 小

优点：生成随机数的速度快，消耗内存小，但得知 seed 的情况下，容易根据随机的区间推断出来

MT

梅森旋转算法是基于二进制字段上的矩阵线性递归 $F_2$，对于一个 k 位的长度，MT 会在[0, $2^k$ - 1] 的区间之间生成离散型均匀分布的随机数，由于周期很长（$2^10037$ - 1）,使得随机数得区间更大，通过对 seed 生成得梅森旋转链进行旋转，处理得到旋转结果，使随机数在区间内均等分布。

因为其优秀得生成随机数速度及内存消耗空间得优化，在多个程序语言中已经使用，如 Python，PHP，Puby等。

BeanDefinition

BeanDefinition 是一个描述 Bean 信息的接口，它描述和定义了一个创建 bean 的所有基本信息，其中就包括了以下属性

1. parentName： 双亲 bean 的名称
2. beanClassName： bean 的类名，但一定有，因为如果该 bean 是由工厂bean 产生的，那么这里的 beanClassName 为空
3. scope： 作用域，如 singleton, prototype
4. lazyInit: 是否为懒加载，如果被设置为 lazy = true，那么这个 bean 会在使用的时候才会被实例化
5. factoryBeanName：生产这个 bean 的工厂名
6. propertyValues： 属性值
7. role： bean 的角色类型，包括了 APPLICATION, SUPPORT, INFRASTRUCTURE
   …
   
   

AbstractDefinition

AbstractDefinition 实现了 BeanDefinition 接口，为子类 RootBeanDefiniton, ChildBeanDefinition, GenericBeanDefinition 提供了 BeanDefinition 公用逻辑的封装，主要封装有以下：

1. 定义了公共的构造函数
2. 为属性值定义了 getter/ setter 等方法，方便获取设置属性值
3. 提供了 overrideFrom() 用于覆盖 当前bean 的定义 及 applyDefaults() 用于设置 bean 的默认属性值

值得一提的是，AbstractBeanDefinition 同时实现了 BeanMetadataAttributeAccessor，即为 BeanDefinition 扩展了以下功能 source, attreibute 等功能：

refresh()

上一篇分析 SpringBoot 启动过程中的 构造过程及 run()，在构造的过程中，主要是根据应用程序的类型设置 WebApplicationType，同时根据 spring.factories的配置读取初始化容器的一些监听器 listeners 和初始化器 initializers。

而在 run()中，主要是对应用上下文 ApplicationContext 创建并进行初始化，设置 WebApplicationType对应的 environment，然后 refreshContext(context) ，最后加载 listeners start(),running 并加入 SpringRunners.

在 refreshContext(context) 主要有下面几个工作：

1. prepareRefresh()
2. prepareBeanFactory()
3. postProcessBeanFactory()
4. invokeBeanFactoryPostProcessors()
5. registerBeanPostProcessors()
6. initMessageSource()
7. initApplicationEventMulticaster()
8. onRefresh()
9. registerListeners()
10. finishBeanFactoryInitialization()
11. finishRefresh()
    
    

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52

  public void refresh() throws BeansException, IllegalStateException {
// 获取监视器锁
      synchronized(this.startupShutdownMonitor) {
      
      	// 刷新上下文前的准备，记录状态，验证必要属性
          this.prepareRefresh();
          ConfigurableListableBeanFactory beanFactory = this.obtainFreshBeanFactory();
          
          // 配置标准的 beanFactory，设置 classloader, bean表达解析器，同时注册重要的bean组件
          this.prepareBeanFactory(beanFactory);

          try {
          	// 模板方法，交由子类对 beanFactory 进行后置处理
              this.postProcessBeanFactory(beanFactory);
              
              // 调用 beanFactoryPostPorcessor 
              this.invokeBeanFactoryPostProcessors(beanFactory);
              
              // 注册容器中的 beanPostProcessors
              this.registerBeanPostProcessors(beanFactory);
              
              // 初始化国际工具类 MessageSource
              this.initMessageSource();
              
              // 初始化并注册事件广播器 ApplicationEventMulticaster
              this.initApplicationEventMulticaster();
              
              // 模板方法，根据应用的具体类型交由子类具体处理，如果是web类型，通常是构建webServer
              this.onRefresh();
              
              // 注册容器中的监听器，包括spring.factories 和 自定义 bean listenr
              this.registerListeners();
              
              // 实例化所有的单例 bean （非 Lazy）,beanPostProcessor 开始起作用
              this.finishBeanFactoryInitialization(beanFactory);
              
              // refresh() 后的额外工作，包括清除resource cahce，注册 LifeCycleProcessor及发布上下文已经刷新的事件 ContexntRefreshedEvent
              this.finishRefresh();
          } catch (BeansException var9) {
		
		// 如果刷新上下文的过程中，出现异常，那么销毁所有已经创建的 bean
              this.destroyBeans();
              
              // 重置 context 的刷新状态，即将 active = false
              this.cancelRefresh(var9);
              throw var9;
          } finally {
          	// 无论失败与否，已经不再需要 bean metadata，重置 Spring 的内核缓存
              this.resetCommonCaches();
          }
      }
  }

SpringApplication.run()

在上一篇中，我们分析了 SpringBoot 启动过程中的 @SpringBootApplocation ，其主要功能就是加载对应的 @Configuration 及 Auto Configure 模块中的组件信息，并将组件内容加入到容器中。

这篇将开始分析 SpringBoot 的启动过程，而启动过程中最核心的两个部分就是 SpringApplication 的启动过程 及 SpringApplication 的 run 方法 ，下面为分析过程：

SpringApplication 的构造函数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

public SpringApplication(ResourceLoader resourceLoader, Class<?>... primarySources) {
	    ...
	    // 设置启动的源Class，即启动的SpringBootLearningApplication.class对象，包含了对应的 classLoader
        this.primarySources = new LinkedHashSet(Arrays.asList(primarySources));
        
        // 设置了 webApplication的类型，尚未配置web，所以当前为 NONE （Servlet, Reactive）
        this.webApplicationType = WebApplicationType.deduceFromClasspath();
        
        // 借助 SpringFactoriesLoader 找到 /META-INF/spring.factories 下的所有配置 key 为 ApplicationContextInitializer 
          （所有的应用初始化器），实例化并设置到 setInitializers 这个集合属性中
        this.setInitializers(this.getSpringFactoriesInstances(ApplicationContextInitializer.class));
        
        // 和上面一样， 通过 SpringFactoriesLoader 找到所有配置 key 为 ApplicationListener (所有的应用程序监听器)，
            实例化并设置到 setListeners 集合属性中
        this.setListeners(this.getSpringFactoriesInstances(ApplicationListener.class));
        
       // 找到 StackTrace （方法调用堆栈）中的 main 方法，即入口类的名字，并 Class.forName 得到类对象
        this.mainApplicationClass = this.deduceMainApplicationClass();
    }

ApplicationEvent

SpringBoot 中使用了很多 Event 去响应容器状态，而 ApplicationEvent 为多个组件 bean 提供了消息通信的支持，其中就包括了接下来在 run( ) 使用到的 SpringApplicationEvent ,它实现了全局的 base ApplicationEvent，并扩展为多个 Spring 启动中的事件 Event，如下：

1. ApplicationContextInitializedEvent
2. ApplicationEnvironmentPreparedEvent
3. ApplicationPreparedEvent
4. ApplicationStartedEvent
5. ApplicationReadyEvent
6. ApplicationFailedEvent
7. ApplicationStartingEvent

事件的传递过程如下：

1. SpringApplicationRunListener 调用对应的操作如 ( starting, running, contextLoad… )
2. SpringApplicationRunListener 内部针对不同的事件，遍历内部集合调用对应的方法，具体实现类为 EventPublishingRunListener 调用
3. EventPublishingRunListener 将对应的操作 ( starting, environmentPrepared.. ) 封装成对应的事件并通过属性 initialMulticaster push 广播出去
4. 最后广播出去的事件如 ( ApplicationStartingEvent ) 会被 SpringApplication 中的 listeners 属性监听处理

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

// SpringApplication.class
public ConfigurableApplicationContext run(String... args) {
	listeners.starting();
}

// SpringApplicationRunListeners 
public void starting() {
        Iterator var1 = this.listeners.iterator();

        while(var1.hasNext()) {
            SpringApplicationRunListener listener = (SpringApplicationRunListener)var1.next();
            listener.starting();
        }
}

// EventPublishingRunListeners.class
public void starting() {
        this.initialMulticaster.multicastEvent(new ApplicationStartingEvent(this.application, this.args));
}

SpringBoot 的启动过程如下：

1
2
3
4
5
6
7

@SpringBootApplication
public class SpringbootlLearningApplication {

    public static void main(String[] args) {
        SpringApplication.run(SpringbootlLearningApplication.class, args);
    }
}

SpringBoot 简化了大量的配置的信息，几行代码就将 Spring Boot 服务启动，具体观察一下，有两部分指的注意：

1. @SpringBootApplication 注解去指定启动类
2. SpringApplication.run(SpringbootLearingApplication.class, args) 启动 Spring 容器

@SpringBootApplication

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

@Target({ElementType.TYPE})
@Retention(RetentionPolicy.RUNTIME)
@Documented
@Inherited
@SpringBootConfiguration
@EnableAutoConfiguration
@ComponentScan(
    excludeFilters = {@Filter(
    type = FilterType.CUSTOM,
    classes = {TypeExcludeFilter.class}
), @Filter(
    type = FilterType.CUSTOM,
    classes = {AutoConfigurationExcludeFilter.class}
)}
)
public @interface SpringBootApplication {
	...
}

可以看到，这里 @SpringBootApplication 是一个组合注解，它包含了以下三个重要的注解：

1. @SpringBootConfiguration
2. @EnableAutoConfiguration
3. @ComponentScan

@SpringBootConfiguration

1
2
3
4
5
6

@Target({ElementType.TYPE})
@Retention(RetentionPolicy.RUNTIME)
@Documented
@Configuration
public @interface SpringBootConfiguration {
}

可以看出，@SpringBootConfiguration 实际上就是一个配置注解，与 @Configuration 不同的是，一个应用程序中只能使用一个 @SpringBootConfiguration，而在我们启动 SpringBootApplication 的时候就已经开启配置，而 @Configuration 可以根据需要进行 JavaConfig 的方式进行多个实例配置

@EnableAutoConfiguration

1
2
3
4
5
6
7
8
9
10
11
12
13

@Target({ElementType.TYPE})
@Retention(RetentionPolicy.RUNTIME)
@Documented
@Inherited
@AutoConfigurationPackage
@Import({AutoConfigurationImportSelector.class})
public @interface EnableAutoConfiguration {
    String ENABLED_OVERRIDE_PROPERTY = "spring.boot.enableautoconfiguration";

    Class<?>[] exclude() default {};

    String[] excludeName() default {};
}

@EnableAutoConfiguration这个复合annotation 的主要作用是开启容器的自动配置功能，而具体由 @AutoConfigurationPackage 和 @Import({AutoConfigurationImportSelector.class}) 实现。

Linux Zero-Copy

什么是零拷贝 ?

Zero Copy 是一种避免 CPU 将数据从一块存储拷贝到另一块存储的技术。 Zero Copy 可以减少数据拷贝和共享总线操作的次数，消除传输数据再存储器之间不必要的拷贝次数，从而有效地提高数据传输地效率。

Linux IO Copy

• read() && write()

当我们在访问一个网页的时候，在 Web Server (Linux) 会调用一下两个 文件读写函数：

1
2

read(fd, buffer, len);
write(sockfd, buffer, len);

过程分析：

1. 调用 read()，将具体的磁盘文件数据读取到 内核（kernel）的文件系统缓冲区中

2. 接着是将 内核缓存区的数据 拷贝到 用户的缓冲区中

3. 调用 write()，将用户缓冲区的数据写入到 内核 socket 的发送缓存区中

4. 在 write() 返回后，内核会将 socket 发送区的数据拷贝到 网卡驱动中

性能分析：

这个过程中，一共发生了四次 I/O copy， 这期间数据按照 kernel -> user -> kernel -> hard drive 的路线，在 内核 到 用户 白白消耗了一圈的 性能开销，同时除了考虑 I/O 的性能开销，还要考虑系统 context switch 带来的开销，当系统调用 read() 时，系统会从 用户态 切换到 内核态，当 read() 返回时，又需要将 内核态 切换到 用户态，同理，write() 也会导致两次的 context switch，也就是说 read() 和 write() 总共会导致 4次的 I/O copy 和 4次上下文切换。

• sendfile()

  而采用 sendfile（）可减少在 read() & write() 所产生的多次 I/O 拷贝和 context switch

1

sendfile(sockfd, fd, NULL, len);

过程分析：

1. 将磁盘中的文件数据拷贝到 内核中的文件缓冲区

2. 向 socket buffer 中 追加 当前的数据在 kernel buffer 中的位置和偏移量

3. 根据 socket buffer 中的位置和偏移量，将 kernel buffer 中的数据 copy 到 网卡驱动中

性能分析：

这次过程中，sendfile() 相比于 read() & write() ，对于将要发送的数据 (socket) ，采用的是记录下对应的 数据在 kernel buffer 中的 位置和偏移量，在最后要发送 socket buffer的数据到网卡设备时，只需通过 位置及偏移量 找到对应 kernel buffer的数据。相比于 read / write， 少了两次 I/O copy，和两次 context switch，性能有了很大的提升。

总结

为什么说是 zero-copy 呢？ 因为在 sendfile() 调用的过程中，对于内核 kernel ，整个过程中是零拷贝的，不涉及 内核到用户之间的数据拷贝。

I / O 模型

I / O 模型的概念大概有：阻塞 / 非阻塞 / 同步 / 异步

1
2
3
4
5
6
7
8
9
10
11
12

一个用户进程发起 I/O 请求的例子：

Linux内核会将所有的外部设备当作一个文件来操作，与外部设备的交互均可等同于对文件进行操作。
即文件的读写都是通过系统调用进行的。

Linux内核通过 file descriptor处理本地文件的读写， socket file descriptor 处理 Socket 网络读写
那么， I/O将会涉及两个系统对象，一个是调用它的用户线程(or thread)，另一个是系统内核 (kernel)

一个读写操作：
1. 用户进程调用 read 方法向内核发起读请求b并等待就绪
2. 内核将要读取的数据复制到文件描述所指向的内核缓存区 （系统准备 IO 数据）
3. 内核将数据从内核缓存区复制到用户的进程空间

阻塞 vs 非阻塞

• 阻塞 ( Blocking IO )：用户发起 I/O 操作后，需要等待其操作完成之后才能继续运行

  • 特点：阻塞式 I/O 模型简单。易于理解，但性能差，会照成用户 CPU 大量闲置
  • 优化：可以采用多线程的方式进行请求调用，但并不能解决根本问题

• 非阻塞 ( No-Blocking IO )：用户进程发起 I/O 操作后，无需等待操作完成，会直接返回调用结果，即如果数据没有准备好，会直接返回失败，这就需要用户进程要定期轮询 I/O 是否就绪

  • 特点：能立即得到返回结果，当使用一个线程去处理 socket 请求，可以极大减少线程数量。但用户线程会不断轮询会增加额外的 CPU 的资源开销

• 总结：阻塞 IO 与 非阻塞 IO 的本质区别主要在于 用户程序是否再等待调用结果（继续等待还是得到结果先处理其他事情）

同步 IO vs 异步 IO

• 同步 IO ( Synchronous IO ) ：当系统内核将处理数据操作准备完毕之后，会主动读取内核数据，用户进程需要等待内核将数据复制到用户进程之后，再进行处理

• IO 多路复用 ( IO- Multiplexing )：可以监视多个描述符，一旦某个描述符读写操作就绪，就可以通知程序进行相应的读写操作

  应用：Linux中使用的 I/O 多路复用机制：select， poll，epoll ( event driven IO），尽管实现的方式不同，但都属于同步 IO，它们都需要在读写事件就绪后，再自己进行读写的操作，内核向用户进程复制数据的过程仍然是阻塞的。

• 特点：尽管使用了事件驱动判断就绪，但与 Blocking-IO 并没有什么太大的不同，甚至在读取的过程中，因为会使用到两个 system call ( select， recvfrom)，相比于 blocking-io 的一个 recvfrom，可能在连接数不高的情况下，性能会更差。但有了 select 的优势就在于系统可以同时处理多个 connnection，效率更高。

• 异步 IO ( Asynchronous IO ) : 当用户进程发起 IO 请求后，会直接返回请求成功，等到再接受到内核的 signal 通知的时候， IO 操作已经完成了

• 非阻塞 ( no-blocking io ) vs 异步io ( asynchronous io )

  no-blocking io：虽然大部分时间都不会 block （loop check data ready），但内核数据准备好之后，还是需要主动调用 recvfrom 系统调用进行数据的复制，这期间 process block

  asynchronous io：整个过程会将任务交由内核处理，直到 IO done，才会向用户进程发送信号通知成功

• 总结：同步 IO 和 异步 IO的本质区别在于内核数据 复制到 用户空间的时候用户线程是否阻塞等待

• 大总结

概念

协变与逆变 (Covariance and contravariance ) 用来描述具有父/子关系的类型通过类型转换之后的继承关系。

即：如果A、B表示类型，f()表示类型转换， 表示子类与父类之间的继承关系，那么有以下定义：
协变(Covariance)：当 A $\subseteq$ B时，f(A) $\subseteq$ f(B)成立；
逆变(contravariance)：当A $\subseteq$ B时，f(B) $\subseteq$ f(A)成立；
不变(invariance)：当A $\subseteq$ B时，以上均不成立，那么f(A)与f(B)之间不存在继承关系；

先定义几个类之间的继承关系

1
2
3
4
5
6

class Fruit{}       // base

class Apple extends Fruit{}

class Lemon extends Fruit{}
class Eureka extends Lemon{}

概念

在面向对象的编程中，装饰器模式是一种设计模式，它允许动态地将行为添加到单个对象，而不会影响来自同一类的其他对象的行为。

举例

当我们在需要扩展一个类的方法的时候，我们需要不断地继承原始方法或上一级方法的类，加上新的方法结构，这样就实现了对于原始方法的增强。当继承关系复杂的情景下，当我们要修改其中一个类方法，会导致其他增强方法的重写，这样使代码的耦合性太强，维护成本很高。对于这种情况，我们可以试试使用装饰者模式去解决这个问题。

就以我们最经常看到的IO操作中，构造一个InputStreamReader，File读取path封装成FileInputStream，接着被装饰成InputStreamReader

1

InputStreamReader reader = new InputStreamReader(new FileInputStream(new File(path)));

概念

在计算机编程中，策略模式是一种行为 软件设计模式，可以在运行时选择算法。代码不是直接实现单个算法，而是接收关于在一系列算法中使用哪些算法的运行时指令。

举例

策略模式可以说是一种选择，它会根据调用者的属性去调用对应的算法，动态地改变对象的行为，用户可以调正对应的策略达到想要的目的。下面会举一个策略模式的Demo场景，同时将分析 Spring 中的策略模式。

组成

Context：一般提供setStrategy(strategy)，用于设置对应的策略，同时起到封装的作用，屏蔽直接访问实际策略。

Srategy：strategy公共接口，规定了策略的属性，方法

ConcreteStrategy：实际策略类，实现了接口，根据具体策略实现对应的算法。